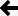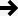Noise signal in XRF and detection limit estimation

In EDXRF practice, detection limit for an element i is customarily calculated by using a signal corresponding to 3 times the standard deviation of the noise signal and the measuring time t_meas. Depending in the theoretical model, other parameters are used to calculate the weight fractions or the mass per unit of area. In the case of analyzing 'thin' samples the detection limits can be calculated as

where S_i (s^-1cm²g^-1) is the instrumental sensitivity for element i.

In the case of analyzing samples of intermediate or infinite thickness the detection limits can be calculated as

where A_i (g cm^-2) is the attenuation correction, which depends on sample effective attenuation coefficient and on sample aerial density.

The main contributions to noise signal N in XRF spectra come from:

• the continuum under the peak (N_cont),
  
  
• a peak observed in a measurement performed for a blank sample (with a net peak area N_blank),
  
  
• a peak observed in the absence of sample (instrumental background, net peak area N_bkg),
  
  
• a spectral interference (net peak area N_SI ).

As the probability distribution of the results of a series of measurements for any of these signals can be considered as close to a Poisson distribution, the value of √N must be estimated in the more general case as